Parameter Study of Channel Flow

Intro

Having a hard time to understand turbulence modelling, I had the idea of exploring how the Reynolds number in channel flow $Re_b=\frac{2\delta U_b}{\nu}$ affects the velocity profile $u(y) \; \forall y \in[0,2\delta]$. So I decided to reuse previous simulation setups for OpenFOAM and explore this further.

Parameters

The parameter study consisted on a exponentially sampled Reynolds numbers usng $b = 100 \cdot 2^a$. For each sample value, a simulation was carried out with cyclic boundary conditions for the inlet/outlet and leveraging symmetry to only solve for the lower part of the channel. A momentum source was added to drive the bulk velocity to the target value.

• Solver: OpenFOAM 7 simpleFoam
• Grid: $4\times50\times1$
• Turbulence model: k-omega-SST
• Bulk velocity $U_b=1$
• Channel length $2\delta = 2$
• Reynolds number $Re \in [100, 36000]$
• Viscosity $\nu = \frac{2 \delta U_b}{Re_b}$

Results

The plot uses:

• First axis: Bulk Reynolds number in log scale $log_{10}(Re_b)$
• Second axis: Distance to lower wall $\frac{x}{\delta}$
• Third axis: Dimensionless velocity $\frac{u}{U_b}$

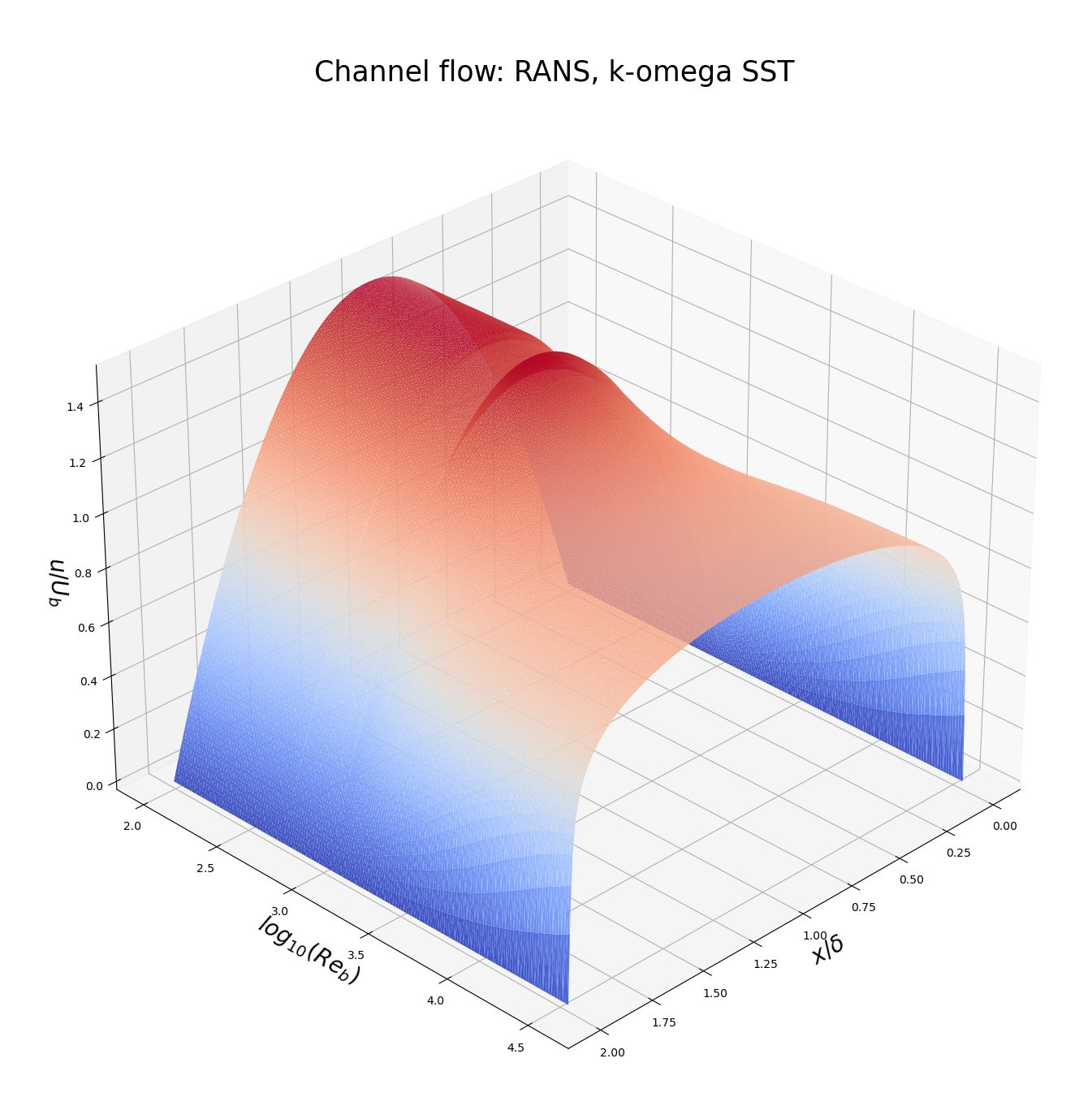
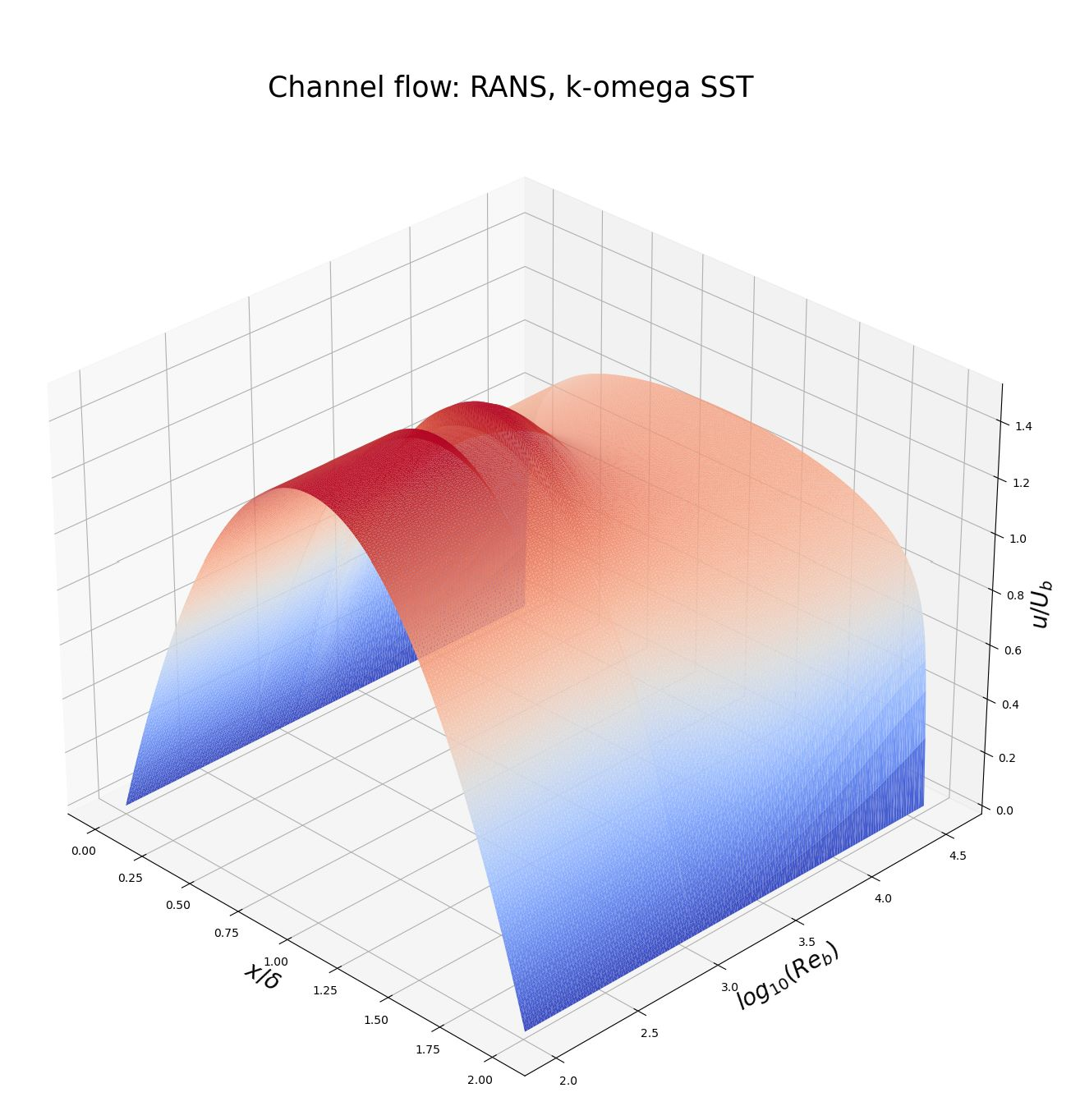
Each slice of the first axis corresponds to a velocity profile of a Reynolds number. At around $Re_b=2100$, the simulation did not converge within the allocated time steps. This can also be seen in the plot.

As an extra task, I decided to print the plot. The file can be found here.